In this work, we give two results that put new limits on distributed quantum advantage in the context of the LOCAL model of distributed computing:

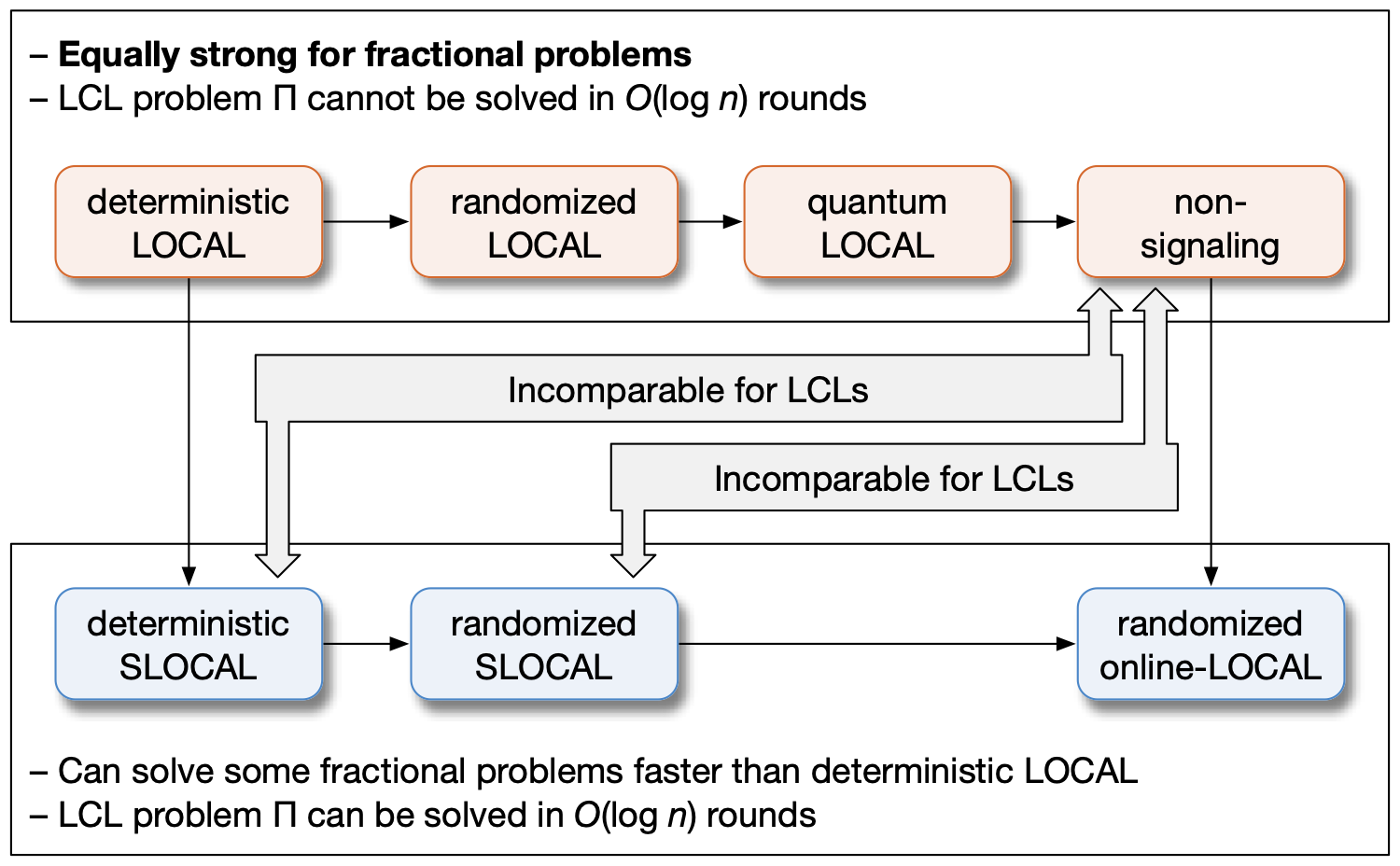
1. We show that there is no distributed quantum advantage for any linear program. Put otherwise, if there is a quantum-LOCAL algorithm $A$ that finds an $\alpha$-approximation of some linear optimization problem $\Pi$ in $T$ communication rounds, we can construct a classical, deterministic LOCAL algorithm $A'$ that finds an $\alpha$-approximation of $\Pi$ in $T$ rounds. As a corollary, all classical lower bounds for linear programs, including the KMW bound, hold verbatim in quantum-LOCAL.
2. Using the above result, we show that there exists a locally checkable labeling problem (LCL) for which quantum-LOCAL is strictly weaker than the classical deterministic SLOCAL model.

Our results extend from quantum-LOCAL also to finitely dependent and non-signaling distributions, and one of the corollaries of our work is that the non-signaling model and the SLOCAL model are incomparable in the context of LCL problems: By prior work, there exists an LCL problem for which SLOCAL is strictly weaker than the non-signaling model, and our work provides a separation in the opposite direction.